令和3年度の都立高校の入試では、出題から除外される内容があります。

新型コロナウイルス感染症の影響で休校が長引いたことに配慮しての措置です。

数学では「三平方の定理」が除外されます。

では、入試問題は簡単になるのでしょうか？

私は必ずしも簡単にはならない、むしろ難しくなる可能性もあると考えています。

令和2年度の入試問題を例に説明します。

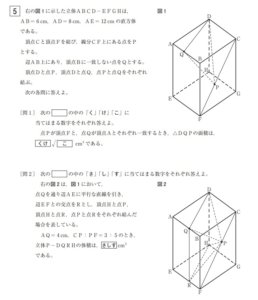
大問題5の空間図形・問2で、直方体の内部に形成される四角錘の体積を求める問題が出ました。

解法は2種類あります。

一つは直方体全体の体積から不要な部分の体積を引いて求める方法です。

この解法では三平方の定理は使いません。

もう一つは三平方の定理を使って四角錘の高さを求める解法です。

私は後者の方が速く確実に解けると感じました。

実際に受験した生徒に尋ねたところ、私と同じ感想でした。

三平方の定理を使わずに空間図形の体積を求めるには、他に等積変形を使う方法もありますが、こちらも難しいです。

令和3年度入試の難易度がどうなるのか、現時点で予測するのは難しい。

ただ、大問題5を確実に取りたい受験生は、三平方の定理を使わない問題を数多く解いておく必要がありそうです。