2月21日に終了した都立高校の前期一般入試。

数学の大問題4、平面図形の「問2－②」の解き方を解説します。

問2－①でAP＝AQが証明されており、∠PAQ＝60度なので、⊿APQは正三角形です。

また⊿ABCと⊿ADBは合同です。

よって⊿BRPと⊿ADBの面積の比を求めればよいことになります。

DP：PB＝２：１ですから、⊿APBは⊿ADBの3分の1です。

次にAからDBに垂線をひき、DBとの交点をSとします。

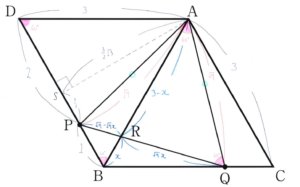
⊿ADPは辺の比が2：1：√3の直角三角形なので、AS＝３√３/2です。

⊿APBに三平方の定理を用いるとＡＰ＝√７となります。

⊿ＢＲＰと⊿ＱＲＡは相似で、相似比は1：√７。

ここでＢＲ＝xとするとＱＲ＝√７x。

また、ＡＢ＝３ですからＡＲ＝３－x、PQ＝√７よりPR＝√７－√７xです。

AR：PR＝1：√７なので代入するとx=2/3を得られ、AR=3－2/3＝7/3。

よってAR：BR＝7：2となり、⊿BRPは⊿APBの面積の9分の２です。

したがって⊿BRPは⊿ADP＝⊿ABCの２７分の２となります。