数学の大問題4、空間図形の「問2」の解き方を解説します。

私は長方形NMPQを底面とし、点Ａからの底面までの距離＝高さを求めて解きました。

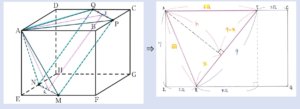
三平方の定理を使ってＮＭ＝４√２、ＰＭ＝９と分かります。

点ＡからＮＭ、ＰＱに垂線を下ろし、交点をそれぞれＲ、Ｓとします。

△ＡＮＭも△ＡＰＱも二等辺三角形ですから、ＲとＳはそれぞれＮＭ、ＰＱの中点です。

したがってＡ、Ｅ、Ｇ、Ｃ、Ｒ、Ｓは同一平面上にあります。

その面を切り取ると右図のようになります。

三平方の定理を使うとＡＲ＝√５７、ＡＳ＝６√２。

さらにＡからＲＳに垂線を引きます。

三平方の定理を使うと、ＡＲ^２－x²＝AS²－（9－x）²（＝h^２）という等式が成り立ちます。

これを解くとx＝11/3となり、再び三平方の定理を使うとh＝14√2/3。

後は底面積×高さ×1/3を計算して、体積＝112ｃｍ³を得られます。